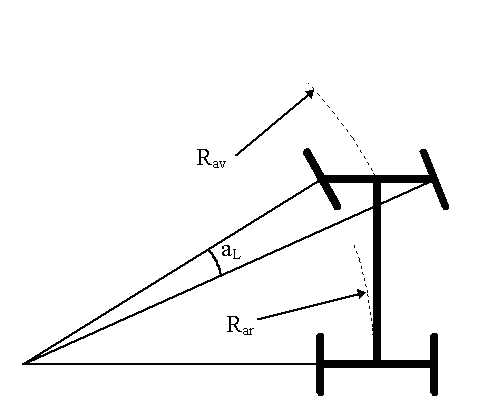
Dans une courbe à très basse vitesse, les efforts latéraux sur les pneus sont négligeables, et le roulis quasiment nul. La condition de non-glissement des roues implique que les roues directrices doivent être braquées d'un angle différent selon qu'il s'agit de la roue intérieure ou de la roue extérieure. C'est l'épure de Jeantaud (ou d'Ackermann pour les anglo-saxons), qui dit, pour simplifier, que le point de centre doit se situer au niveau de l'axe de l'essieu arrière :

L'angle aL qui satisfait la condition de non-glissement est appelé angle de Langensperger. En pratique, la différence de braquage réelle n'est pas strictement égale à aL.Les points milieu de chaque essieu parcourent un cercle de rayon différent, ce qui justifie la présence d'un différentiel central pour les véhicules à quatre roues motrices. On a à basse vitesse, pour des angles de glissement nuls :
Rav2 = Rar2 + L2
où L est l'empattement.
On appelle angle cinématique de braquage l'angle moyen :
acin = arctan (L/Rar) ~ arctan (L/R) ~ L/R
Lorsque la vitesse augmente, des angles de glissement apparaissent, et le centre instantané de rotation se déplace vers l'avant. Rav devient égal à Rar lorsque C a avancé d'un demi-empattement.
Braquages induits par la géométrie de suspension
On utilise souvent, pour les braquages induits par le rebond, un modèle quadratique fonction du débattement zreb :
areb = kreb1 z + kreb2 z2
Dans le cas d'une suspension à triangles superposés, la biellette de direction doit pivoter autour d'un point théorique qui dépend de la géométrie des triangles. Du fait des incertitudes de fabrication, ou si le point théorique n'a pas été recherché dès la conception, un décalage en hauteur ou en longueur entre ce point théorique et le point réel est la cause de ces coefficients kreb1 et kreb2. On a
kreb1 = dH / (LbielLl)
où dH est le décalage en hauteur, Lbiel la longueur de la biellette, Ll la "composante longitudinale" de la longueur de la biellette,
kreb2 = dL / (2LlLideal2)
où dL est le décalage en longueur, et Lideal la longueur idéale de la biellette.
Les braquages induits par le roulis sont considérés comme fonction linéaire de l'angle de roulis :
aroul = kroul \phi
Pour une suspension indépendante, kroul est étroitement lié à kreb, mais est également influencé par la largeur des voies.
Ces angles de braquage se superposent à la pince "statique" définie d'origine. De la pince à l'arrière peut augmenter notablement le sous-virage. A l'avant, alors qu'on pourrait s'attendre au contraire, une pince non excessive augmente également le sous-virage, et améliore la sensation au volant. Mais les réglages de pince sont souvent commandés par des impératifs d'usure. On met généralement un peu d'ouverture sur le train avant des tractions, de manière à ce que l'effort de traction ramène la roue en ligne en roulage normal. Et inversement, la pince est préférée sur les roues non-motrices.
Les angles de carrossage sont également influencés par le rebond et le roulis, et on peut définir les coefficients de proportionnalité correspondants.
A l'arrière, il n'y a pas de braquage induit par le rebond dans le cas d'un "vrai" essieu à bras tirés. Mais il peut devenir considérable dans le cas d'un essieu à bras tirés inclinés, et dépend de l'angle entre le pivot du bras et la ligne médiane du véhicule.
Angles de braquage induits par la flexibilité des éléments de suspension
On décompose généralement la sensibilité des angles de braquage et de carrossage en plusieurs termes dépendant chacun d'une composante des efforts à la roue. Les termes prépondérants viennent des contributions de l'effort latéral et du moment d'auto-alignement.
Ces effets sont évidemment bien plus importants sur des voitures de tourisme que sur des véhicules de compétition, car les exigences de confort et d'absorption amènent à utiliser des liaisons particulièrement souples.