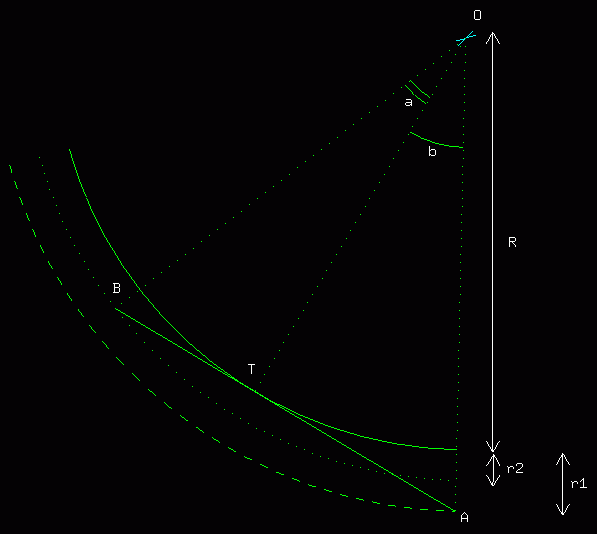
Considérons une motocyclette, de la couleur que vous voulez, de la marque que vous voulez (ça peut même être une Harley), qui aborde un virage dont le rayon de courbure est R. On suppose ce rayon constant, pour la bonne raison que c'est nettement plus simple comme cela. On n'est pas ici pour écrire des choses complètement réalistes, faut pas pousser non plus ...
La voie sur laquelle circule le motocycliste a une largeur r1. Inutile de discuter, c'est moi qui décide. On suppose que ledit motocycliste aborde son virage (en bas du dessin ci-dessous) en un point A, situé sur la ligne médiane pour bénéficier du maximum de visibilité. Faisons l'hypothèse qu'un obstacle lui barre la route en un point B situé au milieu de sa voie. OK, cet obstacle pourrait être aux deux-tiers, ou aux 4/27è de la voie, mais une fois encore c'est moi qui décide, et autant prendre quelque chose de simple. Pis d'abord avec une voie d'environ 3 mètres de large, la moitié correspond à 1m50 ce qui correspond à peu de choses près à la pointe arrière gauche d'une voiture immobilisée au bord de la route. Non mais.

Essayons de déterminer à quelle distance le motard peut apercevoir l'obstacle, et s'il a une chance de s'arrêter compte tenu de la vitesse à laquelle il circule.
Le segment AB est tangent en T au cercle de rayon R. Dans le triangle OTA, on voit que OT = OA.cos(b), soit R = (R+r1).cos(b)
De la même manière, dans le triangle OTB, on a OT = OB.cos(a), soit R = (R+r2).cos(a).
On a donc :
a+b = arccos (R/(R+r2)) + arccos (R/(R+r1))
Avec R = 60 m, r1 = 3 m et r2 = 1.5m, on obtient un angle total (a+b) d'environ 30 degrés. La distance parcourue sur le cercle de rayon R+r1 (là aussi ça n'est pas tout à fait rigoureux puisque le motard plonge progressivement à la corde, mais bon ...) est alors de (R+r1).(a+b) (avec des angles en radians)(ça fait beaucoup de parenthèses)(vous ne trouvez pas ?), soit environ 33.5 mètres.
Ces 33 mètres et des poussières suffisent-ils à s'arrêter quand on arsouille sauvagement ? Suffisent-ils seulement quand on roule sagement ?
Sur un virage de rayon R, la vitesse maxi que l'on peut atteindre correspond environ à une accélération latérale d'1g. Puisque a = v^2/R, on en déduit que v = sqrt(a.R), soit avec a=10 m/s^2 et R=60 m, une vitesse d'environ 24.5 m/s, ou encore 88 km/h.
A cette vitesse là, les 33.5 mètres de marge dont dispose notre arsouilleur correspondent à 1.37 seconde. Inutile de préciser que c'est notoirement insuffisant pour s'arrêter ... En défalquant 0.6 seconde de temps de réaction (notre arsouilleur est hyper concentré et en bonne forme physique ...), cela lui laisse moins de 8 dixièmes pour freiner. Si l'on suppose qu'en courbe il parvient à atteindre une décélération au freinage de l'ordre de 5 m/s^2 (à peu près la moitié d'un très bon freinage en ligne droite, ce qui semble déjà optimiste), il n'aura eu le temps de descendre sa vitesse qu'à environ 20 mètres par seconde, soit 72 km/h, au moment de percuter l'obstacle. Pas bon ...
Bon, arsouiller c'est mal, on en a la preuve, ça peut être dangereux pour la santé. Mais le conducteur auto-proclamé prudent est-il pour autant à l'abri ? Supposons qu'il roule 2 fois moins vite que notre arsouilleur, ce qui en fait déjà quelqu'un de vraiment lent ... (Je ne sais pas si vous avez déjà essayé de quantifier la différence qu'il peut y avoir entre un rythme soutenu et un rythme balade dans votre cas, mais chez moi ça tourne entre 20 et 30% maxi, pas 50 ...) La marge dont il dispose passe donc de 1"37 à 2"74. En le supposant un poil moins concentré que l'arsouilleur sus-mentionné, disons que le temps de réaction de notre touriste fait qu'il lui reste 2 secondes pour freiner. Avec une vitesse initiale de 12.25 mètres par seconde, la décélération moyenne qu'il devra atteindre reste quand même de l'ordre de 6 m/s^2, ce qui me semble, en courbe, carrément optimiste.
Quelques applications numériques complémentaires pour ceux qui ont envie de continuer à jouer :
- avec un rayon de 20 mètres, le secteur angulaire (a+b) mesure environ 51 degrés, et le motard parcourt un arc de 20.5 mètres de circonférence. La vitesse de l'arsouilleur est de 14 m/s (50 km/h), ce qui lui laisse 1"45 de marge. Une fois encore c'est insuffisant pour s'arrêter. Le touriste profite lui de 2"9 de marge, soit un peu plus de 2" de freinage. En arrivant sur l'obstacle à 7 m/s il doit donc pouvoir s'arrêter à temps ...
- en supposant que l'obstacle doit occuper toute la voie pour être vraiment gênant (sinon on peut toujours tenter un évitement ... mais si, puisque je vous dis que ça passe ...), le fait de prendre r2 = 3 m au lieu de 1.5 m change-t-il quelque chose à l'exemple initial ? La marge passe en fait de 33.5 à 39 mètres, ce qui ne change sensiblement rien pour l'arsouilleur (1"58 au lieu d'1"37). Le touriste, lui, bénéficie désormais de 3"2 pour réagir, et doit quand même être capable d'une décélération de 5 m/s^2 pour s'arrêter à temps. J'avoue ne pas avoir d'idée précise de ce que sait faire un motard lambda en courbe, mais je crains que ça ne soit encore au-dessus de ses moyens, surtout en situation d'urgence ...
- la distance parcourue par le motard ne correspond pas exactement à la longueur de l'arc de rayon R+r1,
comme on l'a déjà dit. Mais même en supposant que sa trajectoire suive exactement le segment AB (A =
entrée du virage, T = point de corde, B = sortie), la distance parcourue d est égale à AT+TB. Dans les
deux triangles rectangles OTA et OTB on a AT = sqrt((R+r1)^2 - R^2) et TB = sqrt((R+r2)^2 - R^2).
Avec les mêmes valeurs numériques qu'initialement on obtient 32.7 m au lieu de 33.5 ...