Bien que fidèle lecteur du blog d'Arthur Charpentier je n'avais jusqu'à maintenant fait que zapper ses billets académiques, et notamment ceux concernant l'actuariat. C'est en fait grâce au mathoscope que je suis tombé sur quelques docs relatifs à la théorie du risque (ou théorie de la ruine) _lisibles par un néophyte_. Comme souvent c'est dans les intros des thèses que ça se cache, et il semble que pour un début il soit préférable de lire les choses écrites par/pour les assureurs, moins complexes que les modèles financiers pour lesquels la composante dynamique est primordiale ... Par exemple :




Le modèle de base, dit de Cramer-Lundberg, présente l'avantage d'être accessible à un élève de CM1 (à quelques années près) : une compagnie d'assurance dispose d'un capital initial, qui augmente régulièrement grâce aux cotisations des assurés, mais diminue ponctuellement lors des remboursements de sinistres. La ruine intervient lorsque le montant des réserves tombe à 0 (dans l'exemple suivant à l'instant t4).



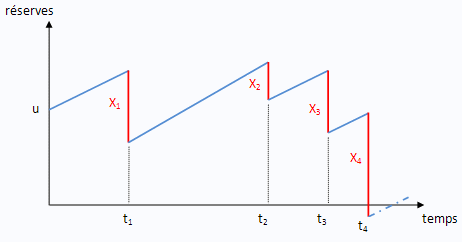
Hypothèses de base :

  • le taux de cotisation c (la pente des segments de droite dans la phase de croissance des réserves) est constant
  • le nombre de sinistres N(t) est un processus de Poisson
  • les montants Xi des sinistres sont des variables aléatoires, supposées indépendantes et identiquement distribuées


Les réserves R à un instant t peuvent être modélisées par le processus suivant (i allant de 1 à N(t)) :

R(t) = u + ct - Σ Xi


On peut alors définir des probabilités de ruine, soit en temps fini T (c'est la probabilité que la ruine intervienne pour t<T), soit en temps infini (c'est la probabilité que la ruine intervienne ... un jour :))

La théorie de la ruine permet ainsi :

  • de quantifier le risque de ruine sous les hypothèses données
  • de déterminer le montant initial à allouer aux réserves pour maintenir le risque de ruine sous un seuil donné, compte tenu du taux de cotisation a priori
  • de déterminer (ou modifier à chaque échéance, via le taux de cotisation) le montant des primes pour maintenir le risque de ruine sous un seuil donné, compte tenu des réserves



(billet en cours de rédaction)


Quelques mots clés :

  • ERM (Enterprise Risk Management)
  • Solvabilité II : réforme règlementaire européenne du secteur de l'assurance, votée en avril 2009, qui fixe notamment de nouveaux objectifs en termes de fonds propres
  • Value at Risk (VaR) : c'est la valeur de la perte (d'un portefeuille financier) qui ne sera pas dépassée avec un seuil de confiance donné
  • Conditional Value at Risk (CVaR) : la VaR ne donnant aucune information sur la perte maximale possible, la notion de CVaR tente de combler ce manque en représentant la moyenne des pertes lorsque celles-ci sont supérieures à la VaR