Victoire ! Un premier jet bien simplifié qui semble fonctionner, sous Matlab.

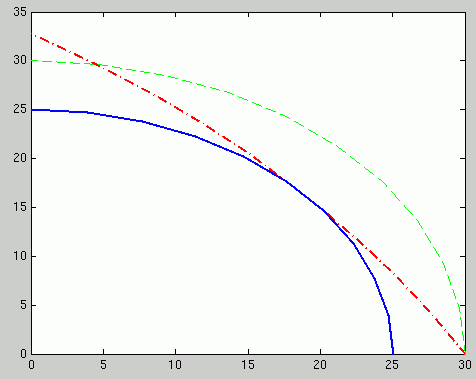
trajectoire sur cercle

En bleu le vibreur intérieur, en vert la ligne "médiane" de la piste, en rouge la trajectoire calculée ...
Il a fallu commencer par du simple, d'où le choix d'un quart de cercle.
Principe :

  • discrétisation du tracé
  • choix des variables du problème d'optimisation : coordonnée orthoradiale (par rapport à la ligne médiane) et norme de la vitesse en chaque point
  • minimisation sous contraintes de la fonction objectif : temps pour parcourir le tracé = somme des temps nécessaires au parcours de chacun des segments = somme des di/vi, où di est la longueur du i-ème segment, et vi la vitesse sur ce même segment

Formulation des contraintes :

  • la distance entre le point courant et la ligne médiane doit être inférieure à la demi-largeur de la piste
  • l'accélération latérale v^2/r, où r est le rayon de courbure instantané, doit être inférieure à une borne supérieure a_max
  • la variation de vitesse entre deux points successifs est limitée par la puissance P du moteur. On peut montrer que vi+1^2-vi^2 < 2.P.di/(m.vi), où m est la masse du véhicule. La puissance disponible est une fonction du régime, donc, sur un rapport donné (oui, je sais ...), de la vitesse.
  • contraintes initiales : position et vitesse (sans spécification de direction ... pour l'instant ?)

Paramètres :

  • rayon du cercle médian (30 m)
  • accélération latérale maximale a_max (10 m/s^-2)
  • "démultiplication"(vitesse = 15 m/s au régime de 4500 tr/min)
  • largeur de la piste (10m)
  • position et vitesse initiales
  • courbe régime-puissance

Fonctions nécessaires :

  • calcul du rayon de courbure d'un cercle inscrit en trois points pour la détermination de l'accélération latérale
  • création d'une fonction puissance=f(vitesse) : on part de la donnée de paires [régime;puissance], puis on approxime par des splines.

Outils :


A faire :

  • connection de bouts de tracé : ligne droite - arc de cercle pour intégrer la notion de freinage dans les contraintes (décélération limite ...), puis arc de cercle - ligne droite - arc de cercle "opposé" pour voir si c'est capable de gérer les changements de courbure de la trajectoire. A terme l'idée est évidemment de parvenir à optimiser la trajectoire sur un tour complet, ce qui permet de s'affranchir de la spécification d'une direction initiale. Enfin, plus ou moins ...
  • intégration d'un modèle de comportement dynamique plus élaboré (...)
  • gérer les discontinuités dues aux changements de vitesse (houla ...). Parce que bon, faire un tour complet sur le même rapport c'est surement très rigolo, mais moyennement efficace. Le problème c'est que je n'ai pour l'instant aucune idée de la manière d'en tenir compte ... Et je me demande même si un changement de stratégie complet (genre en passant à un réseau de neurones) ne serait pas le plus indiqué. Time will tell.